Enigme N° 74
Retrouvez toutes les autres énigmes !

Prévention routière...

Hugo a beaucoup regardé la télé, ces temps-ci... Peut être trop ! Mais il en résulte au moins un point positif : il est maintenant très sensible aux dangers de la circulation automobile !
Il possède, comme sur le schéma, 3 voitures, lesquelles doivent pouvoir se garer indifféremment sur les places de parking 1, 2 ou 3 représentées en bas du dessin.

Il voudrait tracer des routes reliant chaque voiture à chacun des emplacements (soit un total de 9 routes distinctes) afin que chaque véhicule puisse se rendre sur n'importe laquelle de ces places, mais, afin d'éviter les collisions, ces chemins ne doivent en aucun cas se couper, ni être confondus (même partiellement). Ces chemins peuvent passer derrière les parkings et les autos,et avoir n'importe quelle forme, mais ne doivent pas traverser les emplacements (ni bien sûr les autres véhicules).

Comment va faire Hugo, sachant qu'il ne peut construire ni pont, ni tunnel ?

 

Si vous connaissez une énigme amusante ou originale, n'hésitez pas à nous la proposer avec la solution et le nom de l'auteur (si vous le connaissez ; si c'est vous, c'est encore mieux !).
Nous nous ferons un plaisir de la publier dans les semaines à venir !

Proposer une énigme

 

Page d'accueil de Maths à Harry

 

L'énigme de cette semaine est déjà ancienne. Elle m'avait été racontée il y a une vingtaine d'année par ma professeur... de latin (!) et m'a été récemment reproposée par... un de mes élèves !

J'ai passé de longues heures à tenter de résoudre cette énigme lorsque ma professeur me l'a posée, et je ne suis jamais parvenu à trouver une solution. Lorsque mon élève me l'a remémorée, j'ai pris le problème à l'envers pour tenter de prouver (dans la démonstration qui suit) que ce problème est en fait... impossible.

Si l'un d'entre vous pense avoir tout de même trouvé une solution, ou détecte une faille dans le raisonnement, merci de me le signaler !

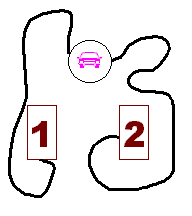
Que se passe-t-il lorsqu'on relie une auto aux garages 1 et 2 ? On obtient un segment de courbe passant par l'auto, commençant au parking 1 et finissant au parking 2 (ou l'inverse).
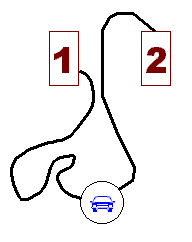
En reliant une deuxième voiture aux garages 1 et 2, on obtient un deuxième segment de courbe (passant par l'auto) de même origine, et de même extrémité.
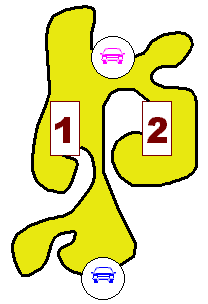
Lorsque deux segments de courbe ont la même origine, la même extrémité, ne se coupent pas et ne sont pas confondus, ils délimitent une "forme fermée" (en jaune sur le dessin).
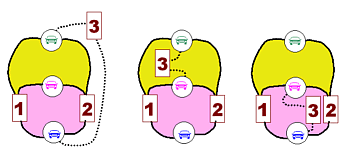
Relions maintenant la voiture verte aux parkings 1 et 2. En schématisant, il n'y a que 3 possibilités (puisqu'on ne veut pas que les routes se croisent), qui chacune aboutissent à la création de deux "formes fermées" (jaune et rose). Bien sûr, l'aspect de chaque courbe pourrait être complètement différent...

Etudions la situation n°1 (les deux autres sont exactement identiques, il suffit de changer la couleur de la voiture) et voyons où peut se situer le parking 3. Il ne peut se situer sur une des courbes car les courbes reliant les parkings doivent être distinctes et qu'un chemin ne peut traverser un parking, ni évidemment à l'emplacement d'une des voitures ou des parkings 1 et 2. Il est donc nécessairement dans la zone jaune, dans la zone rose ou dans la zone blanche (à l'extérieur).

S'il est dans la zone blanche, il n'est pas accessible par la voiture rose (car les zones sont "fermées"). S'il est dans la zone jaune, il ne peut être relié à la voiture bleue. Et dans le dernier cas, il ne peut être relié à la voiture verte.

Donc il est impossible de relier les trois voitures aux trois parkings.

Remarque : lorsque ce problème m'a été posé, il s'agissait de trois maisons à relier au gaz, à l'électricité et au téléphone. Mais le raisonnement est le même !